Home - About AR - Learning Material - Exams - Clubs - Posters
You have probably noticed a plastic speaker cabinet vibrating loudly when a certain frequency is played through it, a washing machine vibrating wildly as the spin cycle passes through a certain speed, etc. This is mechanical resonance, and of course, strings on musical instruments vibrate at a certain notes (frequencies) when struck, plucked, or bowed, depending on thickness, length, and tension.
The electrical equivalent occurs when a capacitor and inductor are in series or parallel, specifically when the capacitive and inductive reactances are equal, expressed as: XL = XC. The frequency can be determined thus: 𝑓 = 1 / (2π √(LC))
This formula applies to both series and parallel circuits, and the resistor value does not come into play. Off the exam, complex
At HF radio frequencies units or 10s of microhenries are used, along with units or 10s of picofarads. These do NOT cancel, so very small numbers, in the range of 10-15 or 10-16 result, although these are restored to a number closer to 10-7 by square-rooting. This requires calculator users to enter values using the exponent key, such as 40 [EEX] 12 [CHS], or 40 [EXP] 12 [±], or the latest Casio, 40 [×10x] 12 [(-)] (confirm in the manual). [±] may be [+/-]
Depending on the device, the final answer may be expressed as a regular number 10015064 (meaning Hz), or 1.015064 07, meaning 1.015064 × 107. Casios have an Engineering Notation button [ENG], which will present results with the exponent in multiples of 3, so your answer might be presented in Megahertz, for example. The figure above would become 10.15064 06, meaning 10.15064×106, or 10.15064 MHz.
While maybe not a perfect analogy, but you have likely been on a swing, and found that by moving your body at the exact right time, you can progressively increase the arc of each swing. Thus is its amplitude, is greater than each single motion of your body can cause. Also, a fairly small motion, when repeated, can maintain the amplitude of the swing.
Likewise, the amplitude of the voltage across capacitor and/or inductor in a series RLC circuit can exceed the stimulating voltage across the whole circuit.
In a parallel RLC circuit at resonance the current consumed by the circuit drops to a minimum, while the circulating current within it reaches its maximum.
At resonance high currents and/or voltages can occur in the circuit.
While not high voltage, the inductor and variable capacitor in a crystal radio select a frequency of resonance, which raises the level of the selected statioin's signal to one which can both pass through a Germanium diode, and drive a small high-impedance earphone. These were often termed a "crystal earpiece", as they contain a peizo element. However, "crystal" in the name of the radio referred to a lump of Galena used to form the diode junction. Modern version use a point contact diode, such as the 1N34, or more often, the 1N34A.
In some cases resonance must be avoided, for instance when placing a power factor correction capacitor across a large mains powered inductive load, as dangerous voltages and currents will develop. In other words, the capacitor must not totally correct the PF. PF is explained on the next page.
There were also fears that an extension to the eastern Australian electrical network, bringing it to around 3000 km, or a half-wave long, taking in north Queensland, and eastern South Australia, would cause it to resonate.
Off the exam, but interesting:
In days of old \ When men were bold \ And light-bulbs were just invented:
When Tungsten lamps replaced carbon ones a popular format was a fairly long tube shaped lamp, with a long U shaped filament, fitted with an Edison Screw base (this was before the very fine spiralling used in modern versions was developed). The problem was that during each half-cycle there was a hot filament with a negative end was in close proximity to a section with a peak voltage of +350 volts on it. Thus were have electrons emitted from this end flowing to the positive area, and the remainder of the U-shaped filament forms a capacitor and an inductor, hairpin shaped sections of wire being used to form a parallel resonant circuit at UHF. This is repeated 100 or 120 times per second, the electron flow alternating in direction. Thus, and RF signal modulated at double the mains frequency would be generated. Evidently it was old 1930s lamps still in use which affected 1950s TVs, indicating that the interference included VHF. The lamps were banned, but worryingly appear to have been recreated for the retro market.
Household LED lamps bought online may cause interference if of poor quality. Quality brand-name products, as well as compact fluorescent units, appear to be of little concern.
No, not a Bond character, but the Quality factor of a resonant circuit. Circuits with high Q have a narrow bandwidth, although in some cases we need to reduce Q to increase bandwidth.
An instrument made from metal, quality wood, or hard plastic generates well defined notes, while a Vuvuzela, made from soft plastic has muddy notes. The former has a high Q, the plastic one, low Q. However, a violin has to have curved body, to provide a wide enough bandwidth, otherwise a single note would be loud and the others indistinct and quiet.
High Q and narrow bandwidth are correlated. "Hy-Q" is a brand of crystal, presumably alluding to their narrow bandwidth response.
This is marked by the lower case Greek letter tau, τ, and signifies the period it takes for a capacitor to reach 63.2% of the applied voltage while charging through a certain resistor. It is determined simply by multiplying the value of the capacitor in Farads by the value of the resistor in ohms.
The same formula can be used to determine the time it takes for a charged capacitor to discharge from its current state of charge to 36.8% of the original voltage.
You will notice these total to 100%, an also that these figures approximate ⅓ and ⅔. The latter is of interest, as 555 timers use three equal resistors as their reference voltages, meaning meaning their time period is 1.1RC ( or 1.1 x R x C).
We can have time constants from very tiny fractions of a second, to 10s of seconds. Excessive time constants can be affected by leakage current in the capacitor.
If we have a 10μF capacitor charged or discharged via a 2.2 MΩ resistor, the TC will be 0.00001 x 2200000, or by cancelling the micro and mega, 10 x 2.2 = 22 seconds. 47 nF x 100 kΩ = 47 x 10-9 x 100 x 103 = 4.7 x 10-3 = 0.0047 s = 4.7 mS. If we double this, for charge and discharge cycles, we get 9.4 mS. Invert this, 1 / 0.0094 ≈ 106.383 Hz, a low audio tone.
At each frequency AC circuits have a specific impedance. This consists of the resistance (R) and reactance (X) which may be either inductive or capacitive. The formula is: Z = √(R2 + X2)
Squaring X makes any signs attached to the j value disappear.
In previous papers we have discussed conductance (G) being the inverse of resistance. As with the factors below, it is measured in Siemens.
G = 1/R, remembering R is Resistance.
The inverse of a value, x, is 1/x. Many calculators feature a [1/x] button. Pressing it after entering 5 should give 0.2, meaning ⅕. Thus 5 ohms in 0.2 Siemens, or 200 mS, not to be confused with 200 ms, being 200 milliseconds. This is also called the reciprocal.
Likewise, the inverse of reactance is susceptance, marked with a B. However, as well as inverting, we change the sign. Remembering that capacitive reactance is signed as negative, the related susceptance is positive; and the positively signed inductive reactance becomes negative susceptance.
Thus, B = -1/X, remembering X is reactance.
Admittance is the inverse of impedance, and it is marked with a Y. It is the vector sum of conductance and susceptance.
Therefore, remembering Z is impedance, Y = 1/Z = 1 / (R + jX) = G + jB.
One of the Wikipedia articles on this topic uses the form Y = Z-1, with raising a value to the power of -1 being an alternative way of writing a reciprocal such as 1/Z.
(Occasionally you will see x½, which is an alternative way to indicate a square root).
Alluded to in a few distractors, reluctance is magnetic resistance. The nature of magnetic materials and structures, such as steel laminations, iron powder, or ferrite is described using this parameter, marked with a cursive R, ℛ.
A purely resistive circuit has the voltage and current in phase (at 0 degrees to each other). Purely inductive and capacitive components have voltage lagging or leading current by by 90 degrees. Real world circuits tend to have some angle, positive or negative, an an intermediate point between 0 and 90 degrees.
The phase angle is expressed in degrees, using the ancient Greek lower-case (closed) phi, thus ϕ, with the upper-case Φ or modern lower-case (open) φ occasionally appearing. Power factor is cos ϕ, varying for 1 to 0. 1 is resistive, 0 purely reactive. Going from cos ϕ to ϕ is via the [COS-1] or [ARC COS] key, usually the alternative function for the [COS] button.
Note that this is NOT (cos x)-1; nor the hyperbolic cosine, obtained using the [cosh] key.
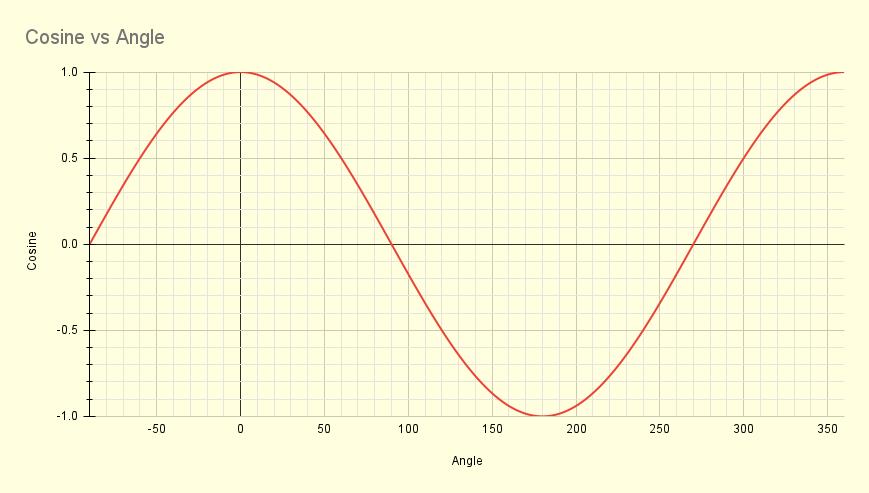
Incidently, in maths ϕ indicates the second angle in a formula, with θ (theta) the first. This lower case theta is used in many publications, such as: Cos θ
 |
| Noting the location of the 0 degree point, you will see that, unlike a sine wave which starts with a value of zero at zero degrees, this starts at the maximum of 1 at 0 degrees, dropping to zero at 90 degrees, before becoming negative until the 270 degree point. It rises to a maximum at 360 degrees. You will notice in the left-most portion that the a negative number of degrees has the same Cosine value as the positive value of the same magnitude. Unfortunately I couldn't get the Google spreadsheet which produced this to place numbers at positions such as 45, 90, and 180 degrees. |
Power-Factor is discussed on the next page.
These are the actual questions from the Extra licence exam pool, as published by the NCVEC.
E5A01
What can cause the voltage across reactances in a series RLC circuit to be higher than the voltage applied to the entire circuit?
A. Resonance
B. Capacitance
C. Conductance
D. Resistance
Typically caused by an inductor and a capacitor in series, these voltages are caused by resonance, answer A.
E5A02
What is resonance in an LC or RLC circuit?
A. The highest frequency that will pass current
B. The lowest frequency that will pass current
C. The frequency at which the capacitive reactance equals the inductive reactance
D. The frequency at which the reactive impedance equals the resistive impedance
Resonance occurs at the frequency at which the capacitive reactance equals the inductive reactance, answer C.
E5A03
What is the magnitude of the impedance of a series RLC circuit at resonance?
A. High, as compared to the circuit resistance
B. Approximately equal to capacitive reactance
C. Approximately equal to inductive reactance
D. Approximately equal to circuit resistance
This is roughly equal to the resistance resistance of the circuit, answer D.
E5A04
What is the magnitude of the impedance of a circuit with a resistor, an inductor and a capacitor all in parallel, at resonance?
A. Approximately equal to circuit resistance
B. Approximately equal to inductive reactance
C. Low, as compared to the circuit resistance
D. Approximately equal to capacitive reactance
This is approximately equal to the circuit's resistance, answer A.
E5A05
What is the result of increasing the Q of an impedance-matching circuit?
A. Matching bandwidth is decreased
B. Matching bandwidth is increased
C. Matching range is increased
D. It has no effect on impedance matching
Higher Q means the bandwidth of the circuit is decreased, answer A.
High-Q is often considered good, but it is possible that the bandwidth of a circuit segment to be too narrow for a voice signal to pass, for example.
E5A06
What is the magnitude of the circulating current within the components of a parallel LC circuit at resonance?
A. It is at a minimum
B. It is at a maximum
C. It equals 1 divided by the quantity 2 times Pi, multiplied by the square root of inductance L multiplied by capacitance C
D. It equals 2 multiplied by Pi, multiplied by frequency, multiplied by inductance
The circulating current within the circuit is at a maximum, answer B.
E5A07
What is the magnitude of the current at the input of a parallel RLC circuit at resonance?
A. Minimum
B. Maximum
C. R/L
D. L/R
Its input current is at a minimum, answer A.
E5A08
What is the phase relationship between the current through and the voltage across a series resonant circuit at resonance?
A. The voltage leads the current by 90 degrees
B. The current leads the voltage by 90 degrees
C. The voltage and current are in phase
D. The voltage and current are 180 degrees out of phase
The inductive reactance and capacitive reactance cancel, so the voltage and current are in phase, as they are in a resistive circuit, answer C.
E5A09
How is the Q of an RLC parallel resonant circuit calculated?
A. Reactance of either the inductance or capacitance divided by the resistance
B. Reactance of either the inductance or capacitance multiplied by the resistance
C. Resistance divided by the reactance of either the inductance or capacitance
D. Reactance of the inductance multiplied by the reactance of the capacitance
This is the resistance divided by the reactance of either the inductance, or of the capacitance, answer C.
E5A10
How is the Q of an RLC series resonant circuit calculated?
A. Reactance of either the inductance or capacitance divided by the resistance
B. Reactance of either the inductance or capacitance times the resistance
C. Resistance divided by the reactance of either the inductance or capacitance
D. Reactance of the inductance times the reactance of the capacitance
This is the reactance of either the inductance or capacitance divided by the resistance, answer A.
E5A11
What is the half-power bandwidth of a parallel resonant circuit that has a resonant frequency of 7.1 MHz and a Q of 150?
A. 157.8 Hz
B. 315.6 Hz
C. 47.3 kHz
D. 23.67 kHz
BW = 7100000 / 150 = 47333.33 ≈ 47.3 kHz, answer C.
E5A12
What is the half-power bandwidth of a parallel resonant circuit that has a resonant frequency of 3.7 MHz and a Q of 118?
A. 436.6 kHz
B. 218.3 kHz
C. 31.4 kHz
D. 15.7 kHz
3700000 / 118 = 31355.9 Hz ≈ 31.4 kHz, answer C.
E5A13
What is an effect of increasing Q in a series resonant circuit?
A. Fewer components are needed for the same performance
B. Parasitic effects are minimized
C. Internal voltages increase
D. Phase shift can become uncontrolled
In a high Q series circuit, the internal voltages increase, answer C.
E5A14
What is the resonant frequency of an RLC circuit if R is 22 ohms, L is 50 microhenrys and C is 40 picofarads?
A. 44.72 MHz
B. 22.36 MHz
C. 3.56 MHz
D. 1.78 MHz
𝑓 = 1 / (2π √(50×10-6 × 40×10-12)) = 1 / (2π √(2×10-15)) = 1 / (2π 4.47214×10-8) = 1 / (2.80993×10-7) = 3.55881×106 ≈ 3.56 MHz, answer C.
Helpfully, it is the only Amateur frequency, and is in the 80 m band. Note that the resistance does not influence the frequency in a simple series or parallel circuit.
E5A15
Which of the following can increase Q for inductors and capacitors?
A. Lower losses
B. Lower reactance
C. Lower self-resonant frequency
D. Higher self-resonant frequency
This is lower loss, answer A.
Ensuring low resistance in inductors, and using high quality capacitors, reduces these losses. Some people silver-plate the tank circuit inductors on power amplifiers, and I have a roller inductor which consists of silver-plated tubing.
E5A16
What is the resonant frequency of an RLC circuit if R is 33 ohms, L is 50 microhenrys and C is 10 picofarads?
A. 23.5 MHz
B. 23.5 kHz
C. 7.12 kHz
D. 7.12 MHz
𝑓 = 1 / (2π √(50×10-6 × 10×10-12)) = 1 / (2π √(5×10-16)) = 1 / (2π 2.236067977×10-8) = 1 / (1.404962922×10-7) = 7.117625×106 ≈ 7.12 MHz, answer D.
Again, it is the only Amateur frequency, a 40 m one. As mentioned, in a simple RLC circuit the R can be ignored.
E5B01
What is the term for the time required for the capacitor in an RC circuit to be charged to 63.2% of the applied voltage or to discharge to 36.8% of its initial voltage?
A. An exponential rate of one
B. One time constant
C. One exponential period
D. A time factor of one
This takes one time constant, answer B.
E5B02
What letter is commonly used to represent susceptance?
A. G
B. X
C. Y
D. B
B, answer D.
This is the negative and reciprocal of Reactance.
E5B03
How is impedance in polar form converted to an equivalent admittance?
A. Take the reciprocal of the angle and change the sign of the magnitude
B. Take the reciprocal of the magnitude and change the sign of the angle
C. Take the square root of the magnitude and add 180 degrees to the angle
D. Square the magnitude and subtract 90 degrees from the angle
You take the reciprocal, and reverse the sign of the angle, answer B.
E5B04
What is the time constant of a circuit having two 220 microfarad capacitors and two 1 megohm resistors, all in parallel?
A. 55 seconds
B. 110 seconds
C. 440 seconds
D. 220 seconds
The two capacitors add to 440 μF, while the two resistors form a 0.5 MΩ resistance, τ = R x C = 500,000 x 0.000440 = 220 seconds, noting that the micro and mega cancel, to give the simpler 440 x 0.5 = 220, answer D.
This is fairly large capacitance for a timing circuit, so these may be a power supply filter capacitors with resistors to discharge the dangerous voltage stored in them.
E5B05
What happens to the magnitude of a pure reactance when it is converted to a susceptance?
A. It is unchanged
B. The sign is reversed
C. It is shifted by 90 degrees
D. It becomes the reciprocal
Discussing the "magnitude" means we are ignoring the sign for the moment, and taking the reciprocal of the value, answer D.
Were the absolute value of the reactive component 35 ohms, we enter 35, and press [1/x] key, giving 0.028571429.
E5B06
What is susceptance?
A. The magnetic impedance of a circuit
B. The ratio of magnetic field to electric field
C. The imaginary part of admittance
D. A measure of the efficiency of a transformer
As the reciprocal of reactance one of the oppositions it is the imaginary (j or -j) part of admittance, answer C.
E5B07
What is the phase angle between the voltage across and the current through a series RLC circuit if XC is 500 ohms, R is 1 kilohm, and XL is 250 ohms?
A. 68.2 degrees with the voltage leading the current
B. 14.0 degrees with the voltage leading the current
C. 14.0 degrees with the voltage lagging the current
D. 68.2 degrees with the voltage lagging the current
Voltage lags the current, with an angle of 14 degrees, answer C.
XC = 500 - 250 = 250 ohms. Z = √(R2 + X2) = √(10002 + 2502) = √(1000000 + 62500) = √1062500 = 1030.7764064 ohms. cos ϕ R / Z = 1000 / 1030.7764064 = 0.97014260. ϕ = 14.0362434669°.
You can also use Z = √(10002 + (500 - 250)2) = √(10002 + 2502), etc
E5B08
What is the phase angle between the voltage across and the current through a series RLC circuit if XC is 100 ohms, R is 100 ohms, and XL is 75 ohms?
A. 14 degrees with the voltage lagging the current
B. 14 degrees with the voltage leading the current
C. 76 degrees with the voltage leading the current
D. 76 degrees with the voltage lagging the current
Voltage lags the current, with an angle of 14 degrees, answer A.
XC = 100 - 75 = 25 ohms. Z = √(R2 + X2) = √(1002 + 252) = √(10000 + 625) = √10625 = 103.07764064 ohms. cos ϕ R / Z = 100 / 103.07764064 = 0.97014260. ϕ = 14.0362°.
You will notice in both cases XC is larger than XL, meaning that the circuit appears capacitive.
E5B09
What is the relationship between the AC current through a capacitor and the voltage across a capacitor?
A. Voltage and current are in phase
B. Voltage and current are 180 degrees out of phase
C. Voltage leads current by 90 degrees
D. Current leads voltage by 90 degrees
Current leads the voltage, by 90 degrees, answer D.
Remember, that if you apply a voltage to a capacitor, it immediately draws a large current, which decays as the capacitor reaches the applied voltage.
E5B10
What is the relationship between the current through an inductor and the voltage across an inductor?
A. Voltage leads current by 90 degrees
B. Current leads voltage by 90 degrees
C. Voltage and current are 180 degrees out of phase
D. Voltage and current are in phase
The voltage leads the current, by 90 degrees, answer A.
Remember that inductors are reluctant (in the general sense) to pass current when a voltage is applied to it, with current slowly building. It is possible to place an inductor in series with a filament lamp, to limit the inrush current.
E5B11
What is the phase angle between the voltage across and the current through a series RLC circuit if XC is 25 ohms, R is 100 ohms, and XL is 50 ohms?
A. 14 degrees with the voltage lagging the current
B. 14 degrees with the voltage leading the current
C. 76 degrees with the voltage lagging the current
D. 76 degrees with the voltage leading the current
Voltage leads current, by 14 degrees, answer B.
XL = 50 - 25 = 25 ohms. Z = √(R2 + X2) = √(1002 + 252) = √(10000 + 625) = √10625 = 103.07764064 ohms. cos ϕ R / Z = 100 / 103.07764064 = 0.97014260. ϕ = 14.0362°.
XL is larger than XC, meaning that the circuit appears inductive.
E5B12
What is admittance?
A. The inverse of impedance
B. The term for the gain of a field effect transistor
C. The turns ratio of a transformer
D. The unit used for Q factor
This the inverse of impedance, answer A.
Note that this involves dangerous voltage and current: Feed a Xenon flash tube with a small capacitor in series with a small inductor, and a large capacitor in series with a large inductor. These are then charged to several hundred volts DC. When the tube is triggered it will draw from the small capacitor, giving a very fast flash, followed by a long flash which builds over perhaps a second, using energy in the large capacitor, moderated by the large inductor. This circuit was designed to test nuclear flash detection circuits.
On to: Electrical Principles 2 - Reactance, Phase, & Power Factor
You can find links to lots more on the Learning Material page.
Written by Julian Sortland, VK2YJS & AG6LE, June 2022.
Tip Jar: a Jefferson (US$2), A$3 or other amount / currency. Thanks!