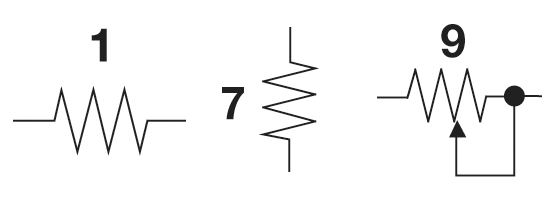Home - About AR - Learning Material - Exams - Clubs - Posters
Amateur Radio Info & Exams - Ohm's Law and Power
For exams 1 July 2018 to 30 June 2022.
Revisions
- = Exactly as 2014 paper
- $ Question & answers unaltered, extra rule added in square brackets
- + Brand new question and number
- - Simplified language
- ^ Edit to fix semantics*
- ≈ Minor change
- ≋ Question / answers restated using "may cause"
- ~ Significant re-writing. With N, answers changed altering letter for correct.
- * New question reusing old number
- ! Existing question renumbered due to deletion of a previous question
- # Renumbered and modified
- ⇅ Renumbered from elsewhere
- ? Answer made less obvious, or more knowledge required, rather than working it out from content
- & Question or Answers enhanced to allow candidate to determine answer from content and logic, rather than knowledge of terminology
*Semantics is the logic of a sentence, and an example of poor semantics is "Fred and another woman", which falsely implies "Fred" is Frederica or Winifred, a female.
Ohm's Law
Ohm's Law and the power calculations are inter-related calculations which can tell us about how energy is being used in a circuit. Each one involves a simply multiplication or division relationship.
Parallel and Series Circuits
At your house the various lights can be switched on and off independently, or perhaps a couple of lights are operated by one switch. Either way, each lamp is in parallel with the others, and in Australia each has 240 volts across it, or 120 volts in the US. Likewise, radios, packet modems, external digital signal processing speakers, and other equipment is placed in parallel across a mains powered 13.8 volt supply, or a battery, and the current summed.
A series circuit is one in which current flows from one device to the next. In old-style Christmas tree lights, typically twenty little 12 volt lamps are in series across 240 volts, meaning no transformer is needed, but removing one lamp means the whole string goes out. Another example is a resister feeding an LED, a red or green LED only needing ~2 volts, so 3 must be dropped if using a 5 volts supply. If a switching a transistor, its voltage drop must be taken into account, especially if the supply voltage is low. A few "white" LEDs can be put in series across a 12 volt supply (with a resistor), as due the the physics of the internal diode junction, each needs around 3 volts (these are usually a blue LED with a yellow phosphor). The same is done in a small neon indicator for your oven, where a high value resistor limits the current through the neon lamp, rated for around 90 volts, and thus 150 volts is dropped in the resistor. Down-under, for some stage lighting, two 120 volt 1000 watt PAR 64 lamps are put in series across 240 volts.
The forward voltage on an LED varies depending on colour, material used, and follows a "curve", so as current rises from 1 mA to 25 mA, it rises by a few tenths of a volt.
Additional Parallel and Series Circuit info for the new Exam
A dude called Kirchhoff worked out some of the basic rules about these circuits. They can be paraphrased as saying that, for DC circuits, the current in all elements of a series circuit is the same, and that the voltage across all components in a parallel circuit is equal. Put a radio and a lamp across a 12 volt battery and both have 12 volts across them. At the component level, if a resistor of the appropriate value and rating feeds a zener diode, it will clamp the voltage at a specific level. If a small load is placed across the diode, then it will have the voltage of the zener applied to it. This is a very simple shunt voltage regulator. The current in the resistor is equal to the sum of that in the zener, and that in the load.
When two components are in parallel, the current flow in each is determined by the value (resistance, etc) of that device. If the devices in parallel are fed from a current source, which can be as simple as a 12 volt battery and a resistor, then the two devices interact more. If two LEDs are placed in parallel, the one with the lowest forward voltage drop will take most or all of the current, which is why LEDs should not be connected this way, as there are variations, even between ones with the same part number. If a current source of 30 mA has a 200 ohm resistor, and a 100 ohm resistor across it, then the 100 ohm one will take two-thirds of the current, the 200 ohm one one-third.
When two are in series, the voltage across each is determined by the relative values, or nature of the devices. A simple example is the voltage divider. In some circuits, rather than the absolute value we get with a zener, or voltage reference diode, we want a percentage of the supply voltage (although we can also take this from a regulated or reference voltage). Beyond the exam, one example is in timing circuits where we want a reference of (about) 63.212% of the supply voltage, as we can easily predict how long a capacitor takes to charge to this percentage of the supply voltage. in one time-constant (τ), by multiplying resistance by capacitance.
At AC or RF frequencies components such as inductors and capacitors in series or parallel can interact in more complex ways; but the answers to the new parallel and series questions remain true.
DC & AC
DC is direct current, where the current travels in one direction only, from positive to negative. This is derived from batteries, or solar panels. Electronic devices require DC.
AC is alternating current, where the current travels backwards and forwards, usually derived from rotating generators. The big benefit is that it is possible to increase or decrease the voltage using transformers.
A simple diode, or diode bridge, is all that is needed to convert the AC output of a transformer to rough DC, with a capacitor to smooth it.
Making AC from DC requires a more complex "inverter" circuit, consisting of an oscillator, and power transistors to switch current through various transformer windings.
Comment on Maths
When I started high school I was a little worried about Algebra, but then I realised that 5 + x = 12 was just a grown up version of 5 + ▢ = 12, and instead of mentally calculating 7 to write it in the box, you rearrange the equation to x = 12 - 5, then x = 7. You will see that on one side I removed, or subtracted, the 5, so on the other I had to subtract 5.
Note however most calculations are multiplication and division.
Power Calculations
If you are in Australia or NZ, you have probably turned over a power board or power strip, and seen "Maximum 240 VOLTS - 10 AMPS - 2400 WATTS", or when buying a heater saw the that the largest retail model was 2400 watts. Why those numbers? The standard (single phase power outlet gives 240 volts (even if it is officially 230 volts with a large upward tolerance), and the standard outlet is rated at 10 amperes, or amps. Multiply those out, and you get the maximum heating capacity, or maximum work a motor can do, 2400 watts. If you are American you would multiply out 120 volts and 15 amps, getting 1500 watts (but there are option to get more power, like 20 amp or larger outlets, or HOT to HOT 240 volt ones; and industrial 277 / 480 volt three-phase).
Voltage is also called "Electromotive Force", or EMF. It is measured in volts, and while battery and mains voltages use units, signals in radio receivers and the like can be millivolts (mV) or microvolts (μV); and voltages inside big valve based power amplifiers and power transmission lines can be kilovolts (kV), or even a megavolt (MV) in the latter case. Higher voltages may require thicker insulation. In formulas voltage is usually represented by E for EMF, except sometimes when a voltage-drop is being calculated, and V is used. Europeans may use U for voltage.
Voltage can also be termed "electrical pressure", as its function is similar to water pressure, driving flow.
For these basic calculations it does not matter if the power is AC or DC.
Current is the flow of electrical charge, noting that while conventional current flows from positive to negative, after this was established, it was found that electrons actually travel from negative to positive. Incidental, while an electrical pulse travels at close to the speed of light, electrons themselves travel fairly slowly. Current is measured in Amperes, or Amps (A), and amp being the transfer of one coulomb per second. Small electronic equipment typically only needs fairly small current, of tens to a few hundred milliamps (mA), while a mobile transceiver 10 to 20-odd amps while transmitting. Starting a car requires hundreds of amps. Kiloamps (kA) are only used on things like smelting aluminium, and the fault current breaking ratings of circuit breakers (for when something goes REALLY wrong). In formulas I is used.
Current has several useful effects. As the electrons collide with others in the material, it heats the material it flows through, a process called Joule heating. Special resistive metal alloys are used to heat air, water, or food. In a toaster it is the radiating infra-red energy which does at least part of the toasting. At high temperatures the wire becomes yellow or white hot, as in a light globe / bulb / lamp. The downside is that even copper wiring can become warm, wasting energy. Another effect is that current generates magnetism, useful in everything from a simple electromagnet (used in solenoids and relays) to meters to motors to most speakers, with the reverse effect used in "dynamic" microphones, converting audio energy to a small electrical signal. Current in special diode junctions produced visible or infra-red light; and through gases, visible or UV light. Certain crystals also deform if current is passed through them (and can generate electrical pulses if struck). There are also electro-chemical effects, useful in things like electroplating, and batteries.
Power is the rate of use of energy, and 1 watt is 1 joule per second. One watt is also 1 volt at 1 amp, or any equivalent, be it 3.3 volts at 300 mA, or 12 volts at 83.3 mA. A wide range of sub-multiple and multiples apply, from femtowatts to gigawatts (as I write this Australia is using somewhat over 25 GW of power). Light globes are marked in watts, based on the power they consume, from tens to a hundreds of watts, to thousands for stage and film lighting. RF power is measured in mW, W, kW or MW, with the power limit for most bands being 1500 watts, or 1.5 kW. Technicians are allowed "only" 200 watts of CW on HF, more than allowed by "full-call" or Advanced licence holders down-under*! Resisters and various semiconductors are also rated by their maximum safe power dissipation. Watts and various multiples can be applied to other things, such as the output of a petrol or diesel engine, given in kW, or even an athlete or cyclist.P is used.
* For Morse code (CW), AM, and FM, the power limit in Oz is 125 watts, with 400 watts peak envelope power (PEP) applying to Single Side Band (SSB).
The formulas, for solving the different values are:
P = I x E
I = P / E
E = P / I
If a charging iDevice draws 2.1 amps at 5 volts, how much power is consumed?
P= I x E
P = 2.1 x 5
P = 10.5 watts.
If a globe is rated at 21 watts at 14 volts (the real voltage in a running car), the current draw is:
I = P / E
I = 21 / 14
I = 1.5 amps.
Suppose you used a clamp meter to test an industrial heater marked 5 kW and found it was drawing 18 amps. What voltage is its supply?
E = P / I
E = 5000 / 18
E = 277.7777 volts
Thus, the supply is nominally 277 volts (the single phase voltage of a US 480 volt delta system).
Watts or Volt-Amps
You will see a transformer rated in VA, rather than watts. This is because with AC the current is not always in phase with the voltage, due to inductive or capacitive loads, and while true power (watts) is less than the apparent power (VA), the A (current) in the calculation does cause I²R heating in the windings (see below). Understanding leading and lagging currents is only required for the Extra paper.
Resistance and Ohm's Law
But what determines how much current flows?
The overall resistance of the circuit determines how much current flows at a certain applied voltage. Resistance in the opposition to the flow of current with in a circuit. Sometimes it is deliberate and desirable, and other times it is not. If we are powering an LED (light emitting diode) we need to limit the current, or the LED has a brilliant, but very short career. In this case we use a resistor made from a film of carbon, or a film of metal, either over a ceramic form. Excess energy is dissipated as heat, but the overall efficiency of a LED is often better than a small lamp, and reliability greater. Larger resistors are made by wrapping wire made from alloys such as nickel and chromium (Nichrome) onto a ceramic form.
Above are the resister symbols used in the examination for sighted candidates, snipped from the circuit diagrams. The first two are fixed resistors, the third a variable resistor, the arrow the wiping terminal moving along the track of resistive material, or from winding to winding of a wire-wound resistance wire coil or toroid, the wire-wound version also called a rheostat (but not in the exam). The device is often called a potentiometer, I think as if you were to put one outer terminal to ground, the other end to, say 10 volts, then the rotating the shaft would vary the voltage on the centre terminal between 0 and 10 volts, that is, varying the potential, as voltage is also called. Likewise, they can be used as a volume control.

Above are three fixed value resistors. An Aussie 5 cent coin is 19.41 mm (a bit over ¾").
- At the top is a beige = carbon film resistor, reading right to left, Brown-Black = 10, Yellow meaning 4 more zeros (or x10 to the 4), so 100,000 or 100 kΩ; Gold meaning ±5% tolerance.
- Below is a blue = metal film one, Orange-Grey-Orange = 383, Black meaning no further zeros (x1, as 10 to the 0 is 1), so 383 ohms, Purple meaning ±0.1% tolerance.
- Last, the military grade DALE resistor is marked 6650F, meaning 665 x 10^0, meaning 665 Ω and from the Internet, F = ±1% tolerance.
Note that any number raised to the power of zero is one.
However, even copper has some resistance, and thus there are limits on how much power a certain size wire can safely carry, lest it overheat, and the insulation smoke or melt. The best conductor is silver, and this is used as a plating in specialised coaxial cable, and in inductors in some high current RF circuits. Isn't gold the best? Nope, it just looks pretty on audiophile connectors. Where high reliability is needed, the resistance to corrosion is valuable. Iron and steel are poor conductors, but stainless can be used in electric fence tape, where high voltage means resistance is not a major problem. Aluminium is not quite as good as copper, but is cheap, even though a greater cross-section is needed. Its use is popular when copper is expensive, but special care must be taken to ensure the natural protective oxide layer is correctly pierced, lest a high-resistance joint is made, which later causes a house fire, etc.
The unit of resistance in the ohm, using the symbol Omega, thus: Ω. As early computers didn't always handle Greek, R was used, or when a multiplier was used, the multiplier was used alone. Also, the decimal is often replaced by the unit, or multiplier. The unit can be used to measure both the resistance of a length of wire, for example, or the resistors mentioned above. In a circuit or notes, a 5.6 ohm resistor may be listed as 5.6Ω, 5.6R, or 5R6; a 2.7 kilohm one listed as 2.7kΩ, 2.7k, or 2k7; and 8.2 megohms can be 8.2M&Omega, 8.2M, or 8M2. Special resistors push up to Gigohms. There are also low resistance resistors, both small electronic components, and large stainless steel or iron units. A 100 milliohm is 100 m&Omega, but may be written 0.1 Ω or 0R1.
A volt will push one amp through a 1 ohm resistor. The formula is:
E = I x R
I = E / R
R = E / I
The proper Irish name of Ireland is EIRÉ, so remember, E=IR.

The diagram above is another memory aid. Cover the value you want to find, and either multiply or divide, depending in whether the remaining symbols are beside or over each other.
Note that I have used / as the division symbol, as often used in computing instead of ÷ for simplicity. I also used a plain x instead of the multiplication symbol, ×. You will also see formulas with the symbols to be multiplied strung one after the other with no symbol, or occasionally with just a dot between them; and in programming, the asterisk, *.
If we wanted to push 2 amps through a 5Ω resistor, we need E = I x R = 2 x 5 = 10 volts.
If we had a 12 volt battery, and connected it to a 2 ohm resistor I = E / R = 12 / 2 = 6 amps.
If we want to run an LED with a forward voltage of 2 volts at 15 mA off a 14 volt supply, we need to drop 12 volts across a resistor. R = E / I = 12 / 0.015 = 800 ohms. We can't buy an 800 ohm resistor, but a common 820 ohm one from a retailer is fine: I = 12 / 820 = 14.634 mA.
There is also a related effect, where current flowing through a (known) resistor causes a certain voltage drop. The 0R1 resistor above, or a similar value may be inserted into a circuit, and by measuring the voltage across the resistor, the current is calculated. In some cases the voltage across such a resistor can be used to cause the circuit to limit current, beyond the effect of the resistor itself. This is useful in an electronics experimenter's benchtop supply, where it is easy enough to short the supply by making a mistake in a circuit being developed.
Suppose a circuit is expected to draw between 0 and 2 amps, then a 0R1 resistor in the negative return will put between 0 and 200mV across the resistor, and a digital "panel meter" can be used to display the current. 0R01 would "shunt" such a meter for 0 to 20 amps. Shunts are also use with many electro-mechanical meters measuring current. High value resistors in series with the meter movement is used when measuring voltage.
Pushing an amp through a length of wire, or the like, and measure the voltage across it, and each millivolt indicates a milliohm.
Impedance
The above applies to DC circuits, and to AC where the load is a pure resistance, but many real-world loads have an inductive aspect, whether motor windings at 50 or 60 Hz mains frequencies, or a speaker coil at audio frequency, or other components at radio frequency. Capacitance also comes into play. This more complex interaction of resistance and reactance is called "impedance", and it is measured in ohms. You may have read about an 8 Ω or 4 ohm speaker. These are all impedance. Coaxial cable has a characteristic impedance, such as 50 Ω or 75 Ω.
Combining the two formulas
It is possible, and often useful to apply one formula, then the other to a problem (as we may want both figures), say to work out the power dissipated by the resistor for the LED above. 0.014634 x 12 volts = 0.17561 W or 175.61 mW. Thus a 1/4 watt resister is adequate, but may run warm. A 1/3 or 1/2 watt unit may be better, and might cost a cent or so more.
However, it is possible to put the two formulas together to do the calculation in one slightly more complex step. As a unit would be applied twice we sometime see squares used, or sometimes square-roots.
If we wanted to know the power dissipated in the resistor from just the current we can derive a formula thus:
P = E x I
P = (I x R) x I
P = I²R
Electricians and power distribution folk talk about these I-squared-R losses. Doubling the current in a feeder quadruples the heating losses, so it may be worth replacing the insulators in a line to allow more power to be passed without increasing the losses.
A bit beyond the test, but a good exercise using parts of it:
Suppose a block of units is built 200 metres from an existing distribution transformer. It requires 48 kW at 240 volts, or 200 amps. Tables show the a cable of 70 mm² is required. It has a resistance using AC (due to skin effect) of 0.1372 ohms for the 400 m loop. P = 200² x 0.137 = 40000 x 0.137 = 5488 watts, the power used by several heaters wasted! The voltage drop, E = 200 / 0.1372 = 27.44 volts. This means a large variation in brightness of lamps as peoples heaters, air-conditioners, cookers, etc, kick in and out.
Instead, lets install a transformer at the site, fed with 11,000 volt lines. I = 48000 / 11000 = 4.36 amps, call it 4.4 as the transformer is not 100% efficient (but that loss would have occurred in the existing transformer anyway). Thin wire, just 2.5 mm² has a resistance of 3.604 ohms for the loop. P = 4.4² x 3.604 = 69.77 watts. E = 4.4 / 3.604 = 1.22 volts, a tiny fraction of the 11 kV so load variations will have little or no impact on lamp voltage.
The above is an exercise, in the real world is is possible that 415/240 volt three-phase cables may be run from the existing transformer, and while losses would be still be high, they would be lower, as current would be split over the phases. The 11 kV would also likely be a three phase arrangement, although there are certainly rural arrangements where two of the three phases wires are split off to a property, going to a pole-transformer between these phases, rather than a singe phase and neutral going to the "pole-pig" in the US system.
In heavy industrial settings and large telephone exchanges heavy copper "bus-bars" are used instead of cables. A 12.7 mm x 127 mm (1/2" x 5") copper bus-bar can carry over 2000 amps. The large surface area compared to a round cable helps dissipate heat, and also "skin-effect" has lower effect, so current carrying capacity is better than the round cable. Aluminium and Brass are also used.
* Skin effect is the tendency of AC current to travel towards the surface of conductors. It starts to kick in at mains frequency (50 or 60 Hz) and becomes more significant at radio frequencies, hence copper clad steel working as well for upper HF antennas, as well as inside coax cable for VHF and UHF TV, etc.
Many amateur radio transceivers run on 12-14 volts, (or "13.8 volts"), so they can be used in cars, or powered from a separate mains powered supply. To get 100 watts RF output they might need 150 watts to 200 watts, depending on the efficiency of the radio, P = 150 / 12 = 12.5 amps to P = 200 / 12 = 16.666 amps. Wires need to be run from the car's battery, or from a power supply, in either case, with at least one fuse, maybe a few connectors, etc, and these all add voltage drops. Just because the current in a wire does not make the insulation smoke does not mean that its voltage drop will be low enough for the application.
Fairly light 2.5 mm² wire can carry the current, and there is a 6 metre loop to the battery, the resistance is 0.04446 ohms. V = 20 x 0.8892 = volts, with about 100 mV for fuses, etc; and there is at least a volt of drop.
Substitute 6mm cable, with a resistance of 0.01848 ohm, so V = 20 x 0.01848 = 0.3698 volts.
So, while the wires supplied with radios will safely carry the required current, the voltage drop can be more than desirable, especially if running from the battery of a car without the engine running.
At 240 volts 10 or 20 amps only requires fairly light wire, as dropping a few volts is only a percent or so of the overall voltage, which does not affect the performance of the load.
In high voltage DC power supplies sometimes a high value "bleeder" resistor is placed across the high voltage capacitor, a component which smooths the ripples in the rectified output of the transformer to make the DC as pure as possible, but which can store a lethal charge for perhaps hours, just waiting to get the technician or tinkerer, to discharge this charge once the device is off. Lets suppose 400 volt supply has a 100 μF capacitor with a 470 kΩ resistor across it, which would reduce the voltage to a safe level after a few 47 second "time constant" periods. What is the power in the resistor as the device operates?
We want to know power, P, from E and R. While we could calculate the current (851 μA), and from this power, we can derive a single line formula thus:
P = E x I
P = E x (E / R)
P = E² / R
Thus P = E² / R = 400² / 470000 = 160000 / 470000 = 0.3404 watts. At this power the resistor would run hot, and is at some risk of failing, so a 1 watt or greater resistor should be selected.
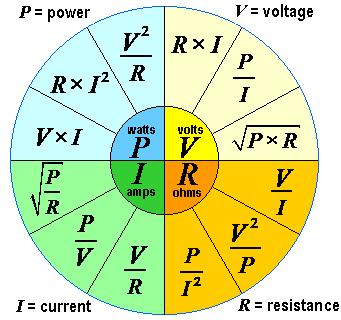
A more complex formula wheel, by "VampireBaru".
Example series and parallel circuits
 |
Left: A simple parallel circuit, where IT = I1 + I2. If the battery is 12 volts, then the voltage across each resistor is 12 volts. This likewise applies if the resistors were instead a radio and a lamp. If the battery is large, and well charged, then how much current the radio draws has very little impact on the voltage on the lamp, and therefore its brightness.
Centre Left: A simple series circuit, where the current through both devices is the same, and depends on the total resistance, say 2 + 10 = 12 ohms, meaning 1 amp would flow were it a 12 volt battery. The voltage is divided depending on the values of each resistor, with these values, it is 2 and 10 volts, totalling the 12 of the battery.
Centre Right: A more complex series-parallel circuit, but not a recommended one, as we cannot be sure of how well the current will be shared. Were the battery 12 volts, and the resistor 250 ohms, then about 40 mA would be available to the LEDs. If the forward voltage curves are identical, then it would be shared perfectly, 20 mA each. If one is red, at about 2 volts VF and the other is blue, with a 3 volt VF, the red one will pull the voltage to 2 volts, below the point the blue will draw any, and so all of the 40mA will flow in the red one, probably shortening its life. If the LEDs are similar, then one might take the voltage down to 1.9 volts, at which point the other will still conduct some current, maybe only 10 mA while the first uses 30. This demonstrates the interaction of two parallel devices in a circuit where current is restricted by a resistor.
Right: Another kind of energy source is the current source, which attempts to maintain a constant current in its load. One can be made using an LM317 variable voltage regulator IC and a resistor, the current in this resistor setting the current in the circuit. The '317 is really a 1.25 volt regulator, and this maintains 1.25 v between the output and adjust terminal, so 12.5 ohms means 100 mA flows. This circuit could be used to power one or more higher powered LEDs in series, maintaining the current reasonably independent of the VF, and of the voltage drop in the wires to it or them. This circuit demonstrates that available current is shared depending on the relative values of the two parallel components. The two resistors in parallel is 1/(1/90 + 1/180) = 60 ohms, and so the voltage across them is 6 volts. |
MHz
One new question in this section asks you to apply the metric M for Mega, and Hz for Hertz, the unit for frequency to get MHz, as used in 27 MHz (CB), 100.1 MHz (FM radio), 144 MHz (2 metres), or 477 MHz (UHF CB). In is important to note the capital or upper-case "M", likewise the upper- and lower-cases in Hz. A small "m" has a significantly different meaning, 1 milliHertz is one cycle per 16 minutes, 40 seconds (!), or 3.6 per hour, although the term is more often used
Relevant Questions
These are the actual exam questions relating to this knowledge.
T5C08=
What is the formula used to calculate electrical power in a DC circuit?
A. Power (P) equals voltage (E) multiplied by current (I)
B. Power (P) equals voltage (E) divided by current (I)
C. Power (P) equals voltage (E) minus current (I)
D. Power (P) equals voltage (E) plus current (I)
Remember back to the first example - the biggest figure of 240 V, 10 A and 2400 W is the 2400 W, so it must be multiplication, so A. You will also note that this is the first time you have seen addition or subtraction on this page (apart from the LED voltage drop.
T5C09=
How much power is being used in a circuit when the applied voltage is 13.8 volts DC and the current is 10 amperes?
A. 138 watts
B. 0.7 watts
C. 23.8 watts
D. 3.8 watts
Remember you can discard the addition and subtraction, so the choice is 0.7 watts - way too small; or multiply 13.8 by 10 and get the 138 watts, as per P = I x E. Answer A.
T5C10=
How much power is being used in a circuit when the applied voltage is 12 volts DC and the current is 2.5 amperes?
A. 4.8 watts
B. 30 watts
C. 14.5 watts
D. 0.208 watts
Chuck out the addition; and remember we are after power (P), having been given E and I, so we multiply, getting 2 12s (=24), plus a half of 12 (=6), giving 30, so B. P = E x I = 12 x 2.5 = 30. Answer B.
T5C11=
How many amperes are flowing in a circuit when the applied voltage is 12 volts DC and the load is 120 watts?
A. 0.1 amperes
B. 10 amperes
C. 12 amperes
D. 132 amperes
Different, we are after current (I), given Power (P) and voltage (E), so time to divide, but which way? Given P = E x I, we need to get rid of the E from the I side, meaning we divide P by E on the other. I = P / E, = 120 / 12 = 10 amperes, answer B.
T5C12-
What is impedance?
A. A measure of the opposition to AC current flow in a circuit
B. The inverse of resistance
C. The Q or Quality Factor of a component
D. The power handling capability of a component
As resistance is the opposition to DC current, impedance is the opposition to the flow of AC current, so answer A. By the way, the inverse of resistance is conductance, measured in Siemens, something not otherwise in the exams. Q is related to resonant circuits (you'll get to that on more advanced papers); and power ratings of resisters, etc is measured in watts.
T5C13≈
What is a unit of impedance?
A. Volts
B. Amperes
C. Coulombs
D. Ohms
If impedance is a little like resistance, the answer just might be Ohms. But check: Volts are for voltage, Current is in Amperes, and Coulombs is a unit for charge. Yep, the answer must be D. Also remember speakers and coax marked in ohms.
T5C14+
What is the proper abbreviation for megahertz?
A. mHz
B. mhZ
C. Mhz
D. MHz
M for Mega, Hz for Hertz; so MHz, answer D.
T5D01=
What formula is used to calculate current in a circuit?
A. Current (I) equals voltage (E) multiplied by resistance (R)
B. Current (I) equals voltage (E) divided by resistance (R)
C. Current (I) equals voltage (E) added to resistance (R)
D. Current (I) equals voltage (E) minus resistance (R)
Chuck out the addition and subtraction. E = I x R, so flip that around to I = E / R. Answer B.
T5D02=
What formula is used to calculate voltage in a circuit?
A. Voltage (E) equals current (I) multiplied by resistance (R)
B. Voltage (E) equals current (I) divided by resistance (R)
C. Voltage (E) equals current (I) added to resistance (R)
D. Voltage (E) equals current (I) minus resistance (R)
Again, give the "added" and "minus" options the heave-ho. Get your Gaelic on, and remember EIRé, so it is E = I x R, answer A.
T5D03=
What formula is used to calculate resistance in a circuit?
A. Resistance (R) equals voltage (E) multiplied by current (I)
B. Resistance (R) equals voltage (E) divided by current (I)
C. Resistance (R) equals voltage (E) added to current (I)
D. Resistance (R) equals voltage (E) minus current (I)
A high-school transposition question: We know E = I x R, and we need to move the I to the other side to get R. As it is a multiplication relationship, we need to divide it by I, to cancel it out, and what you do on one side you must do on the other, so on that side we get E / I, tidy the order up, and you get R = E / I, answer B.
T5D04=
What is the resistance of a circuit in which a current of 3 amperes flows through a resistor connected to 90 volts?
A. 3 ohms
B. 30 ohms
C. 93 ohms
D. 270 ohms
You need to find R from I and E, so flip E = I x R to R = E / I = 90 / 3 = 30 ohms, so B.
T5D05=
What is the resistance in a circuit for which the applied voltage is 12 volts and the current flow is 1.5 amperes?
A. 18 ohms
B. 0.125 ohms
C. 8 ohms
D. 13.5 ohms
Like the previous R = E / I = 12 / 1.5 = 8. So, C. As a check, the current is over 1 amp, so the resistance must be less than 12 ohms, but if it was below one ohm, then the current would be (well) over 12 amps.
T5D06=
What is the resistance of a circuit that draws 4 amperes from a 12-volt source?
A. 3 ohms
B. 16 ohms
C. 48 ohms
D. 8 ohms
Another "Find R from E and I", so R = E / I = 12 / 4 = 3 ohms, answer A. You will notice they have put in addition and subtraction answers for those who haven't been paying attention; and a multiplication, but put 48 ohms in a 12 volt circuit, and not much current will flow, a quarter amp (250 mA) to be precise.
T5D07=
What is the current flow in a circuit with an applied voltage of 120 volts and a resistance of 80 ohms?
A. 9600 amperes
B. 200 amperes
C. 0.667 amperes
D. 1.5 amperes
This isn't a "Do destructive things with stupidly large currents" You-Tube channel, so not A. Even 200 amps is unusual in Ham radio (and it is an addition answer, so probably wrong).
R = I x E so I = E / R = 120 / 80 = 12 / 8 = 3 / 2 = 1.5 amps, answer D.
By the way, 120 volts is the nominal mains voltage for lower powered equipment in North America.
T5D08
What is the current flowing through a 100-ohm resistor connected across 200 volts?
A. 20,000 amperes
B. 0.5 amperes
C. 2 amperes
D. 100 amperes
Another I = E / R, just with the position of the values changed. So, I = 200 / 100 = 2 / 1 = 2 amps. Too easy! C.
T5D09=
What is the current flowing through a 24-ohm resistor connected across 240 volts?
A. 24,000 amperes
B. 0.1 amperes
C. 10 amperes
D. 216 amperes
Another "Find I from E and R", so I = E / I = 240 / 20 equals 10 amps, answer C. For Aussies, this is roughly what your multimeter would say if you tested a 2400 watt heater.
Why 240 volts in America? Most US homes are supplied with "split-phase" power, where the pole transformers are what electronics folk call "centre tapped", with this centre tap connected to ground / earth, forming the neutral; giving 120 volts from one hot to neutral for iThingy chargers, lamps, and smaller radios, but 240 volts between the the hots for things like clothes dryers, and for Amateurs, 1500 watt output linear amplifiers, which require power not only for the RF output, but for the filament supply of the big valves, and for fans, etc.
Where would the 100 or 200 amps be seen? Probably in a large inverter based supply which generates higher voltages to run a 1500 watt amplifier. Since this would require extra batteries, and probably a second alternator, smarter folk would make the set-up at least 24 volts, to make the current a little more sensible. Very large transmitters, such as HCJB's HC100, a 100kW unit used for global shortwave broadcasting might draw 220 amps per phase at 480 volts (delta), some transformed down to power the filament in the main valve, drawing 300 amps at 10 volts AC. R = 10 / 300 = 0.0333 Ω or 33.3 μΩ, so a pretty chunky filament.
T5D10=
What is the voltage across a 2-ohm resistor if a current of 0.5 amperes flows through it?
A. 1 volt
B. 0.25 volts
C. 2.5 volts
D. 1.5 volts
E = I x R = 0.5 x 2 = 1, so A.
T5D11=
What is the voltage across a 10-ohm resistor if a current of 1 ampere flows through it?
A. 1 volt
B. 10 volts
C. 11 volts
D. 9 volts
E = I x R = 1 x 10 = 10, so B.
T5D12=
What is the voltage across a 10-ohm resistor if a current of 2 amperes flows through it?
A. 8 volts
B. 0.2 volts
C. 12 volts
D. 20 volts
E = I x R = 2 x 10 = 20, so D.
T5D13+
What happens to current at the junction of two components in series?
A. It divides equally between them
B. It is unchanged
C. It divides based on the on the value of the components
D. The current in the second component is zero
A dude called Kirchhoff once said that the sum of current entering a node or junction is the same as the current leaving it, so when the junction has two connections these current are the same - there is no change, answer B.
T5D14+
What happens to current at the junction of two components in parallel?
A. It divides between them dependent on the value of the components
B. It is the same in both components
C. Its value doubles
D. Its value is halved
The current is divided between the two components, depending on the value and type of the components, answer A.
T5D15+
What is the voltage across each of two components in series with a voltage source?
A. The same voltage as the source
B. Half the source voltage
C. It is determined by the type and value of the components
D. Twice the source voltage
The voltage across each is determined by the value and type of the components, answer C. This can be a simple sharing of the voltage, if it is two resistors in series, this depending on their value. If one is a zener diode, then you might have, say 5.1 volts across this component, and the remainder of the voltage across the resistor feeding it, even when the voltage of the source changes.
T5D16+ (D)
What is the voltage across each of two components in parallel with a voltage source?
A. It is determined by the type and value of the components
B. Half the source voltage
C. Twice the source voltage
D. The same voltage as the source
Put a radio and a lamp across a 12 volt battery (or a Ham transceiver and a CB) and both have 12 volts across them, so it is the same as the source voltage, answer D.
That wasn't too hard, was it?
On to: Component Symbols & Schematic Diagrams
You can find links to lots more on the Learning Material page.
Written by Julian Sortland, VK2YJS & AG6LE, February 2018.
Tip Jar: a Jefferson (US$2), A$3 or other amount / currency. Thanks!