Home - About AR - Learning Material - Exams - Clubs - Posters
You have probably noticed a plastic speaker cabinet vibrating loudly when a certain frequency is played through it, an unbalanced washing machine vibrating wildly as the spin cycle passes through a certain speed, etc. This is mechanical resonance, and of course, strings on musical instruments vibrate at a certain notes (frequencies) when struck, plucked, or bowed, depending on thickness, length, and tension.
The electrical equivalent occurs when a capacitor and inductor are in series or parallel, specifically when the capacitive and inductive reactances are equal, expressed as: XL = XC. The frequency can be determined thus: 𝑓 = 1 / (2π √(LC))
This formula applies to both series and parallel circuits, and the resistor value does not come into play.
At HF radio frequencies units or 10s of microhenries are used, along with units or 10s of picofarads. These do NOT cancel, so very small numbers, in the range of 10-15 or 10-16 result, although these are restored to a number closer to 10-7 by square-rooting. This requires calculator users to enter values using the exponent key, such as 40 [EEX] 12 [CHS], or 40 [EXP] 12 [±], or the latest Casio, 40 [×10x] 12 [(-)] (confirm in the manual). [±] may be [+/-]
Depending on the device, the final answer may be expressed as a regular number 10015064 (meaning Hz), or 1.015064 07, meaning 1.015064 × 107. Casios have an Engineering Notation button [ENG], which will present results with the exponent in multiples of 3, so your answer might be presented in Megahertz, for example. The figure above would become 10.15064 06, meaning 10.15064×106, or 10.15064 MHz.
While maybe not a perfect analogy, you have likely been on a swing, and found that by moving your body at the exact right time, you can progressively increase the arc of each swing. Thus the amplitude is greater than any single motion of your body can cause. Also, a fairly small motion, when repeated, can maintain the amplitude of the swing.
Likewise, the amplitude of the voltage across capacitor and/or inductor in a series RLC circuit can exceed the stimulating voltage across the whole circuit.
In a parallel RLC circuit at resonance the current consumed by the circuit drops to a minimum, while the circulating current within it reaches its maximum.
At resonance high currents and/or voltages can occur in the circuit.
While not high voltage, the inductor and variable capacitor in a crystal radio select a frequency of resonance, which raises the level of the selected station's signal to one which can both pass through a Germanium diode, and drive a small high-impedance earphone. These were often termed a "crystal earpiece", as they contain a peizo element. However, "crystal" in the name of the radio referred to a lump of Galena used to form the diode junction. Modern version use a point contact diode, such as the 1N34, or more often, the 1N34A.
In some cases resonance must be avoided, for instance when placing a power factor correction capacitor across a large mains powered inductive load, as dangerous voltages and currents will develop. In other words, the capacitor must not totally correct the PF. PF is explained on the next page. In bridges resonance can result in problems ranging from user discomfort to collapse. The Millennium Bridge in London required dampers to be fitted. The driverless Metro in Sydney suffers from all sorts of shakes and wobbles, partly down to being a 60 km/h device operated at 100 km/h.
There were also fears that an extension to the eastern Australian electrical network, bringing it to around 3000 km, or a half-wave long, taking in north Queensland, and eastern South Australia, would cause it to resonate.
Off the exam, but interesting:
In days of old \ When men were bold \ And light-bulbs were just invented:
When Tungsten lamps replaced carbon ones a popular format was a fairly long tube shaped lamp, with a long U shaped filament, fitted with an Edison Screw base (this was before the very fine compound spiralling used in modern versions was developed). The problem was that during each half-cycle there was a hot filament with a negative end was in close proximity to a section with a peak voltage of +350 volts on it. Thus we have electrons emitted from this end flowing to the positive area, with the remainder of the U-shaped filament forming a capacitor and an inductor, hairpin shaped sections of wire being used to form a parallel resonant circuit at UHF. This is repeated 100 or 120 times per second, the electron flow alternating in direction. Thus, and RF signal modulated at double the mains frequency would be generated. Evidently it was old 1930s lamps still in use which affected 1950s TVs, indicating that the interference included VHF. The lamps were banned, but worryingly appear to have been recreated for the retro market.
Household LED lamps bought online may cause interference if of poor quality. If you are the importer into Australia of a Temu grade lamp which cause interference ACMA gets grumpy at you. If you add a few to an Element 14 or RS order they are the importer, but they are CE marked. Likewise lamps added to a parts order from TME in Poland should be fine, as they are genuinely CE marked. Quality brand-name products, as well as compact fluorescent units, appear to be of little concern.
No, not a Bond character, but the Quality factor of a resonant circuit. Circuits with high Q have a narrow bandwidth, although in some cases we need to reduce Q to increase bandwidth.
An instrument made from metal, quality wood, or hard plastic generates well defined notes, while a Vuvuzela, a horn made from soft plastic, has muddy notes. The former has a high Q, the plastic one, low Q. However, a violin has to have curved body, to provide a wide enough bandwidth, otherwise a single note would be loud and the others indistinct and quiet.
High Q and narrow bandwidth are correlated. "Hy-Q" is a brand of crystal, presumably alluding to their narrow bandwidth response.
The maths are that if you divide the centre frequency by the bandwidth you get the Q. 100 MHz and a -3 dB (half power) bandwidth of 1 MHz you have a Q of 100. The examiner however asks for the bandwidth from a named Q. Thus if we wanted to listen to 102.5 MHz and a filter had a Q of 150 we could calculate an overall bandwidth of 0.6833333333 MHz, or 683.333 kHz. This would pass the full bandwidth of an art music station, while significantly attenuating a C-RAP station on 96.1 MHz, or a wall-of-noise station on 104.9 MHz. It would however pass signals from a rural station on 102.7 MHz.
"Art music" is the more formal term (and Library of Congress Subject Heading) for classical music, as it continues to be composed today, well beyond the Classical period.
In a parallel RLC circuit Q is calculated by dividing resistance by the reactance of either the inductance or capacitance.
This is marked by the lower case Greek letter tau, τ, and signifies the period it takes for a capacitor to reach 63.2% of the applied voltage while charging through a certain resistor. It is determined simply by multiplying the value of the capacitor in Farads by the value of the resistor in ohms.
The same formula can be used to determine the time it takes for a charged capacitor to discharge from its current state of charge to 36.8% of the original voltage.
You will notice these total to 100%, an also that these figures approximate ⅓ and ⅔. The latter is of interest, as 555 timers use three equal resistors as their reference voltages, meaning meaning their time period is 1.1RC (or 1.1 x R x C).
We can have time constants from very tiny fractions of a second, to 10s of seconds. Excessive time constants can be affected by leakage current in the capacitor. Using a divider (eg 4017) after the 555 can give longer times.
If we have a 10μF capacitor charged or discharged via a 2.2 MΩ resistor, the TC will be 0.00001 x 2200000, or by cancelling the micro and mega, 10 x 2.2 = 22 seconds. 47 nF x 100 kΩ = 47 x 10-9 x 100 x 103 = 4.7 x 10-3 = 0.0047 s = 4.7 mS. If we double this, for charge and discharge cycles, we get 9.4 mS. Invert this, 1 / 0.0094 ≈ 106.383 Hz, a low audio tone.
At each frequency AC circuits have a specific impedance. This consists of the resistance (R) and reactance (X) which may be either inductive or capacitive. The formula is: Z = √R² + X², typed more easily as √(R2 + X2)
Thus if we had rectangular notation for an impedance of 38+17j ohms we could Z = √38² + 17² = √1444 + 289 = √1733 = 41.629316593, or about 41.6 ohms, which would not get an SWR meter swinging too far (1.605:1). See: Calculator on Cheandy website. They make some useful small amplifiers. OH1TV's one agrees.
To find the angle use: 17/38 = 0.44736842105. Arctan 0.44736842105 or tan-1 0.44736842105 = 24.1022345 degrees. Ensure your calculator is in Degrees mode.
Squaring X makes any signs attached to the j value disappear.
Imagine a university quadrangle with a grassed area 30 by 40 metres, which the roped off at most times. This is because instead of walking the linear addition of 70 metres, any student can see that walking diagonally is shorter. A maths or surveying student will say that the vector addition for the direct path is D = √(402 + 302) = √(1600 + 900) = √2500 = 50 metres.
Some find the diagram below very helpful to understand the concept. You can see the 9 and 16 squares on the left and bottom sides, and the 25 squares on the slope, or hypotenuse. 9 + 16 = 25. Thus the square root values, being the lengths must be 3, 4, and 5.

Thanks to the Alberta Government for the image. From: Pythagorean Theorem
Ropes, cords, or rods in a 3 : 4 : 5 proportion have been used for millennia to lay out buildings.
Real world calculations will often result in values which provide a square root which is a decimal, which can he rounded as appropriate.
Speakers are another place impedance matters. Many projects and small radios use a 57 mm speaker of 8 Ω, and a rating of 1 watt or less. However, older germanium transistor radios or phonograph (vinyl record) players used 27 ohm speakers to allow less current for the same power. Other values are 4 and 16 ohms, with 4 being common in car audio as it allowed greater power from 12 volts. Such inductances are a combination of the DC resistance or the copper, and the inductive reactance of the coil. Apparently interaction between the cone and the cabinet can affect impedance across the audio band, compared to a bare speaker is free air, just as loading a motor alters its power consumption and power factor. Element 14 (Farnell) has a 64 ohm speaker with a cone diameter of 60 mm in their "multicomp PRO" range, stamped ALTAI.
These figures are "polar" meaning that a value includes an impedance (or susceptance) value, and an angle between plus and minus 90 degrees, even if we are not indicating that angle at the moment.
I used to work with a land surveyor at times, and the "theodolite" or rather Total Station, which included distance measurement could be used to either record a point during a "detail" survey, say the location of an existing driveway; or place a mark such as a property or building corner. This consisted of a precise angle, and a distance. A lot of the calculations, such as converting from rectangular to polar coordinates could be completed in a BASIC program on an HP palmtop PC.
Older germanium era radios often used 9 volt batteries, rather than the two 1.5 volt cells typically used in the silicon era. Silicon transistors or some IC amplifiers can drive lower impedances happily. As headphones need to use far less power, Walkman style headphones are often 32 ohms.
In previous papers we have discussed conductance (G) being the inverse of resistance. As with the factors below, it is measured in Siemens, with the symbol S.
Millisiemens and microsiemens are also used, mS and μS. Seconds use the lowercase s. This used to be expressed using the term "mho" with the symbol being an upside-down Omega, ℧. Transconductance in valves, FETs and bipolar transistors are measured in mS, with older valve datasheets using micromhos, μ℧. However, talk of FETS in distractors below are just that, wrong answers.
Some multimeters have mS, μS and nS ranges.
G = 1/R, remembering R is Resistance.
The inverse of a value, x, is 1/x. Many calculators feature a [1/x] button. Pressing it after entering 5 should give 0.2, meaning ⅕. Thus 5 ohms in 0.2 Siemens, or 200 mS, not to be confused with 200 ms, being 200 milliseconds. This is also called the reciprocal.
Likewise, the inverse of reactance is susceptance, marked with a B. However, as well as inverting, we change the sign. Remembering that capacitive reactance is signed as negative, the related susceptance is positive; and the positively signed inductive reactance becomes negative susceptance.
Thus, B = -1/X, remembering X is reactance.
The exam terms susceptance as the "imaginary part of admittance" as it is the j or "imaginary" part of the complex number.
Admittance is the inverse of impedance, and it is marked with a Y. It is the vector sum of conductance and susceptance.
Therefore, remembering Z is impedance, Y = 1/Z = 1 / (R + jX) = G + jB.
One of the Wikipedia articles on this topic uses the form Y = Z-1, with raising a value to the power of -1 being an alternative way of writing a reciprocal such as 1/Z.
(Occasionally you will see x½, which is an alternative way to indicate a square root).
Alluded to in a few distractors, reluctance is magnetic resistance. The nature of magnetic materials and structures, such as steel laminations, iron powder, or ferrite is described using this parameter, marked with a cursive R, ℛ.
A purely resistive circuit has the voltage and current in phase (at 0 degrees to each other) with a PF of 1. Purely inductive and capacitive components have voltage lagging or leading current by 90 degrees (PF = 0). Real world circuits tend to have some angle, positive or negative, an an intermediate point between 0 and 90 degrees.
The phase angle is expressed in degrees, using the ancient Greek lower-case (closed) phi, thus ϕ, with the upper-case Φ or modern lower-case (open) φ occasionally appearing. Power factor is cos ϕ, varying for 1 to 0. 1 is resistive, 0 purely reactive. Going from cos ϕ to ϕ is via the [COS-1] or [ARC COS] key, usually the alternative function for the [COS] button.
Note that this is NOT (cos x)-1; nor the hyperbolic cosine, obtained using the [cosh] key.
Incidently, in maths ϕ indicates the second angle in a formula, with θ (theta) the first. Thus lower case theta is used in some publications, such as: Cos θ
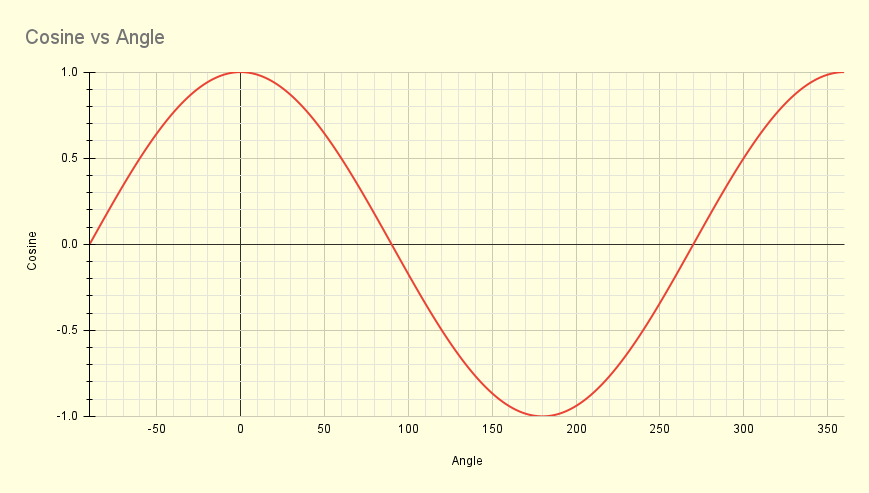
 |
| Noting the location of the 0 degree point, you will see that, unlike a sine wave which starts with a value of zero at zero degrees, this starts at the maximum of 1 at 0 degrees, dropping to zero at 90 degrees, before becoming negative until the 270 degree point. It rises to a maximum at 360 degrees. You will notice in the left-most portion that the a negative number of degrees has the same Cosine value as the positive value of the same magnitude. Unfortunately I couldn't get the Google spreadsheet which produced this to place numbers at positions such as 45, 90, 180, and 270 degrees. |
Reactive power and power factor is discussed more on the next page, although some power-factor question have been pulled. If you press the [COS] button on the 24.1022345 degrees above you get 0.9128182519, which is a good power factor. You'd write 0.9 or 0.91.
In a circuit having a power factor of 0.71 and apparent power is 500VA the power consumed is calculated thus:
Multiply the PF by the VA value, P = 0.71 x 500 = 355 watts.
Power, in watts, must be less that or equal to the VA figure, as PF cannot exceed 1 (perfectly resistive).
This would occur with an angle of (just under) 45 degrees, famous for being 1/√2 ≈ 0.70710678118.
PF is probably something of more interest to the broadcast system design technician than the the average ham. While domestic billion does not take power factor into account, to the consumer's benefit. For commercial sites (perhaps including repeaters) the supply authority will charge based on the wattless inductive current, which they must still provision for: Depending where you live, you may notice transformers in the street marked in kVA, not kW.
Not on the exam: When a motor or a transformer is lightly loaded the power factor rises. WW2 RAAF transmitters had larger than necessary transformers to increase reliability, meaning a poor PF. In anything from commercial motors to fluorescent lamps in schools and offices to substation transformers require power factor correction capacitors. Note that older ones can contain, and perhaps leak, PCBs, a toxic oily "forever chemical". In a broadcast site a large blower might need such a capacitor, and potentially a proper motor starter.
These are the actual questions from the Extra licence exam pool, as published by the NCVEC.
E5A01
What can cause the voltage across reactances in a series RLC circuit to be higher than the voltage applied to the entire circuit?
A. Resonance
B. Capacitance
C. Low quality factor (Q)
D. Resistance
Typically caused by an inductor and a capacitor in series, these voltages are caused by resonance, answer A.
E5A02
What is the resonant frequency of an RLC circuit if R is 22 ohms, L is 50 microhenrys and C is 40 picofarads?
A. 44.72 MHz
B. 22.36 MHz
C. 3.56 MHz
D. 1.78 MHz
𝑓 = 1 / (2π √(50×10-6 × 40×10-12)) = 1 / (2π √(2×10-15)) = 1 / (2π 4.47214×10-8) = 1 / (2.80993×10-7) = 3.55881×106 ≈ 3.56 MHz, answer C.
Helpfully, it is the only Amateur frequency, and is in the 80 m band. Note that the resistance does not influence the frequency in a simple series or parallel circuit.
E5A03
What is the magnitude of the impedance of a series RLC circuit at resonance?
A. High, as compared to the circuit resistance
B. Approximately equal to capacitive reactance
C. Approximately equal to inductive reactance
D. Approximately equal to circuit resistance
This is roughly equal to the resistance resistance of the circuit, answer D.
E5A04
What is the magnitude of the impedance of a circuit with a resistor, an inductor and a capacitor all in parallel, at resonance?
A. Approximately equal to circuit resistance
B. Approximately equal to inductive reactance
C. Low compared to the circuit resistance
D. High compared to the circuit resistance
This is approximately equal to the circuit's resistance, answer A.
E5A05
What is the result of increasing the Q of an impedance-matching circuit?
A. Matching bandwidth is decreased
B. Matching bandwidth is increased
C. Losses increase
D. Harmonics increase
Higher Q means the bandwidth of the circuit is decreased, answer A.
High-Q is often considered good, but it is possible that the bandwidth of a circuit segment to be too narrow for a voice signal to pass, for example.
E5A06
What is the magnitude of the circulating current within the components of a parallel LC circuit at resonance?
A. It is at a minimum
B. It is at a maximum
C. It equals 1 divided by the quantity 2 times pi, times the square root of (inductance L multiplied by capacitance C)
D. It equals 2 times pi, times the square root of (inductance L multiplied by capacitance C)
The circulating current within the circuit is at a maximum, answer B.
E5A07
What is the magnitude of the current at the input of a parallel RLC circuit at resonance?
A. Minimum
B. Maximum
C. R/L
D. L/R
Its input current is at a minimum, answer A.
E5A08
What is the phase relationship between the current through and the voltage across a series resonant circuit at resonance?
A. The voltage leads the current by 90 degrees
B. The current leads the voltage by 90 degrees
C. The voltage and current are in phase
D. The voltage and current are 180 degrees out of phase
The inductive reactance and capacitive reactance cancel, so the voltage and current are in phase, as they are in a resistive circuit, answer C.
E5A09
How is the Q of an RLC parallel resonant circuit calculated?
A. Reactance of either the inductance or capacitance divided by the resistance
B. Reactance of either the inductance or capacitance multiplied by the resistance
C. Resistance divided by the reactance of either the inductance or capacitance
D. Reactance of the inductance multiplied by the reactance of the capacitance
This is the resistance divided by the reactance of either the inductance, or of the capacitance, answer C.
E5A10
What is the resonant frequency of an RLC circuit if R is 33 ohms, L is 50 microhenrys and C is 10 picofarads?
A. 7.12 MHz
B. 23.5 kHz
C. 7.12 kHz
D. 23.5 MHz
𝑓 = 1 / (2π √(50×10-6 × 10×10-12)) = 1 / (2π √(5×10-16)) = 1 / (2π 2.236067977×10-8) = 1 / (1.404962922×10-7) = 7.117625×106 ≈ 7.12 MHz, answer A.
Again, it is the only Amateur frequency, a 40 m one. As mentioned, in a simple RLC circuit the R can be ignored.
E5A11
What is the half-power bandwidth of a parallel resonant circuit that has a resonant frequency of 7.1 MHz and a Q of 150?
A. 157.8 Hz
B. 315.6 Hz
C. 47.3 kHz
D. 23.67 kHz
BW = 7100000 / 150 = 47333.33 ≈ 47.3 kHz, answer C.
E5A12
What is the half-power bandwidth of a parallel resonant circuit that has a resonant frequency of 3.7 MHz and a Q of 118?
A. 436.6 kHz
B. 218.3 kHz
C. 31.4 kHz
D. 15.7 kHz
3700000 / 118 = 31355.9 Hz ≈ 31.4 kHz, answer C.
E5A13
What is an effect of increasing Q in a series resonant circuit?
A. Fewer components are needed for the same performance
B. Parasitic effects are minimized
C. Internal voltages increase
D. Phase shift can become uncontrolled
In a high Q series circuit, the internal voltages increase, answer C.
E5B01
What is the term for the time required for the capacitor in an RC circuit to be charged to 63.2% of the applied voltage or to discharge to 36.8% of its initial voltage?
A. An exponential rate of one
B. One time constant
C. One exponential period
D. A time factor of one
This takes one time constant, answer B.
E5B02
What letter is commonly used to represent susceptance?
A. G
B. X
C. Y
D. B
This is "B", answer D.
This is the negative and reciprocal of Reactance.
E5B03
How is impedance in polar form converted to an equivalent admittance?
A. Take the reciprocal of the angle and change the sign of the magnitude
B. Take the reciprocal of the magnitude and change the sign of the angle
C. Take the square root of the magnitude and add 180 degrees to the angle
D. Square the magnitude and subtract 90 degrees from the angle
You take the reciprocal, and reverse the sign of the angle, answer B.
E5B04
What is the time constant of a circuit having two 220 microfarad capacitors and two 1 megohm resistors, all in parallel?
A. 55 seconds
B. 110 seconds
C. 440 seconds
D. 220 seconds
The two capacitors add to 440 μF, while the two resistors form a 0.5 MΩ resistance, τ = R x C = 500,000 x 0.000440 = 220 seconds, noting that the micro and mega cancel, to give the simpler 440 x 0.5 = 220, answer D.
This is fairly large capacitance for a timing circuit, so these may be a power supply filter capacitors with resistors to discharge the dangerous voltage stored in them.
E5B05
What happens to the magnitude of a pure reactance when it is converted to a susceptance?
A. It is unchanged
B. The sign is reversed
C. It is shifted by 90 degrees
D. It is replaced by its reciprocal
Discussing the "magnitude" means we are ignoring the sign for the moment, and taking the reciprocal of the value, answer D.
Were the absolute value of the reactive component 35 ohms, we enter 35, and press [1/x] key, giving 0.028571429 Siemens, or around 28.57 mS.
E5B06
What is susceptance?
A. The magnetic impedance of a circuit
B. The ratio of magnetic field to electric field
C. The imaginary part of admittance
D. A measure of the efficiency of a transformer
As the reciprocal of reactance it is the imaginary (j or -j) part of admittance, answer C.
E5B07
What is the phase angle between the voltage across and the current through a series RLC circuit if XC is 500 ohms, R is 1 kilohm, and XL is 250 ohms?
A. 68.2 degrees with the voltage leading the current
B. 14.0 degrees with the voltage leading the current
C. 14.0 degrees with the voltage lagging the current
D. 68.2 degrees with the voltage lagging the current
Voltage lags the current, with an angle of 14 degrees, answer C.
XC = 500 - 250 = 250 ohms. Z = √(R2 + X2) = √(10002 + 2502) = √(1000000 + 62500) = √1062500 = 1030.7764064 ohms. cos ϕ R / Z = 1000 / 1030.7764064 = 0.97014260. ϕ = 14.0362434669°.
You can also use Z = √(10002 + (500 - 250)2) = √(10002 + 2502), etc
E5B08
What is the phase angle between the voltage across and the current through a series RLC circuit if XC is 300 ohms, R is 100 ohms, and XL is 100 ohms?
A. 63 degrees with the voltage lagging the current
B. 63 degrees with the voltage leading the current
C. 27 degrees with the voltage leading the current
D. 27 degrees with the voltage lagging the current
Voltage lags the current, with an angle of 63 degrees, answer A.
XC = 300 - 100 = 200 ohms. Z = √(R2 + X2) = √(1002 + 2002) = √(10000 + 40000) = √50000 = 223.60679775 ohms. cos ϕ R / Z = 100 / 223.60679775 = 0.4472135955. ϕ = 63.4349488°.
You will notice in both cases XC is larger than XL, meaning that the circuits appears capacitive.
It is also helpful to note that where the reactive component exceeds the resistive component the angle exceeds 45 degrees, as here. Where X is less thar R the angles is under 45 degrees.
E5B09
What is the relationship between the AC current through a capacitor and the voltage across a capacitor?
A. Voltage and current are in phase
B. Voltage and current are 180 degrees out of phase
C. Voltage leads current by 90 degrees
D. Current leads voltage by 90 degrees
Current leads the voltage, by 90 degrees, answer D.
Remember, that if you apply a voltage to a capacitor, it immediately draws a large current, which decays as the capacitor reaches the applied voltage.
E5B10
What is the relationship between the AC current through an inductor and the voltage across an inductor?
A. Voltage leads current by 90 degrees
B. Current leads voltage by 90 degrees
C. Voltage and current are 180 degrees out of phase
D. Voltage and current are in phase
The voltage leads the current, by 90 degrees, answer A.
Remember that inductors are reluctant (in the general sense) to pass current when a voltage is applied to it, with current slowly building. It is possible to place an inductor in series with a filament lamp, to limit the inrush current.
E5B11
What is the phase angle between the voltage across and the current through a series RLC circuit if XC is 25 ohms, R is 100 ohms, and XL is 75 ohms?
A. 27 degrees with the voltage lagging the current
B. 27 degrees with the voltage leading the current
C. 63 degrees with the voltage lagging the current
D. 63 degrees with the voltage leading the current
Voltage leads current, by 27 degrees, answer B.
XL = 75 - 25 = 50 ohms. Z = √(R2 + X2) = √(1002 + 502) = √(10000 + 2500) = √12500 = 111.803398875 ohms. cos ϕ R / Z = 100 / 111.803398875 = 0.894427191. ϕ = 26.5650512°.
XL is larger than XC, meaning that the circuit appears inductive.
You can see that the X component is small compared to the R, so the angle is small!.
E5B12
What is admittance?
A. The inverse of impedance
B. The term for the gain of a field effect transistor
C. The inverse of reactance
D. The term for the on-impedance of a field effect transistor
This the inverse of impedance, answer A.
The last option is logically stupid, as one is the inverse of the other.
Ensuring low resistance in inductors, and using high quality capacitors reduces losses in tuned circuits, to increase Q. Some people silver-plate the tank circuit inductors on power amplifiers. I have a roller inductor which consists of silver-plated tubing, taken from something like the automatic tuner in a naval transmitter. Silver mica capacitors may be used for fixed values.
Note that this involves lethally dangerous voltage and current: Feed a Xenon flash tube with a small capacitor in series with a small inductor, and a large capacitor in series with a large inductor. These are then charged to several hundred volts DC. When the tube is triggered it will draw from the small capacitor, giving a very fast flash, followed by a long glow which builds over perhaps a second, using energy in the large capacitor, moderated by the large inductor. This circuit was designed to test nuclear flash detection circuits.
On to: Electrical Principles 2 - Reactance, Phase, & Power Factor
You can find links to lots more on the Learning Material page.
Written by Julian Sortland, VK2YJS & AG6LE, July 2025.
Tip Jar: a Jefferson (US$2), A$3 or other amount / currency. Thanks!
You can also buy me a non-coffee beverage: ko-fi.com/ag6le